Stationary
저번에 마지막에 약간 다뤘는데 다시 한 번 살짝 짚고 넘어가면
보통 아래 3가지를 만족하면 stationary data입니다.
1) 데이터의 평균이 상수인 경우
2) 데이터의 분산이 상수인 경우
3) 계절성이 존재하지 않는 경우
그리고 이중에서도 특히, 데이터의 평균이 0인 경우는 특별하게, white noise라고 합니다.
눈으로 확인하는 것보다는 Adfuller test (ADF) 를 진행해보는 것이 가장 정확할 것입니다.
ARMA 모델에 데이터를 넣기 위해서는 해당 데이터가 stationary 해야하기 때문에 다시 한 번 stationary 에 대해 정리했습니다.
PACF
저번 포스트(?) 에서 ㅋㅋACF에 대해서는 다뤘는데 PACF에 대해서는 다루지 않았는데
PACF는 partial auto correlation fuction을 입니다. ACF는 t기의 정보를 예측할 때 lag 까지의 (직접, 간접) 정보를 모두 사용하는 반면, PACF는 t기의 정보를 예측하는데 lag에서 t기 까지의 직접적인 정보만을 사용한다고 합니다.
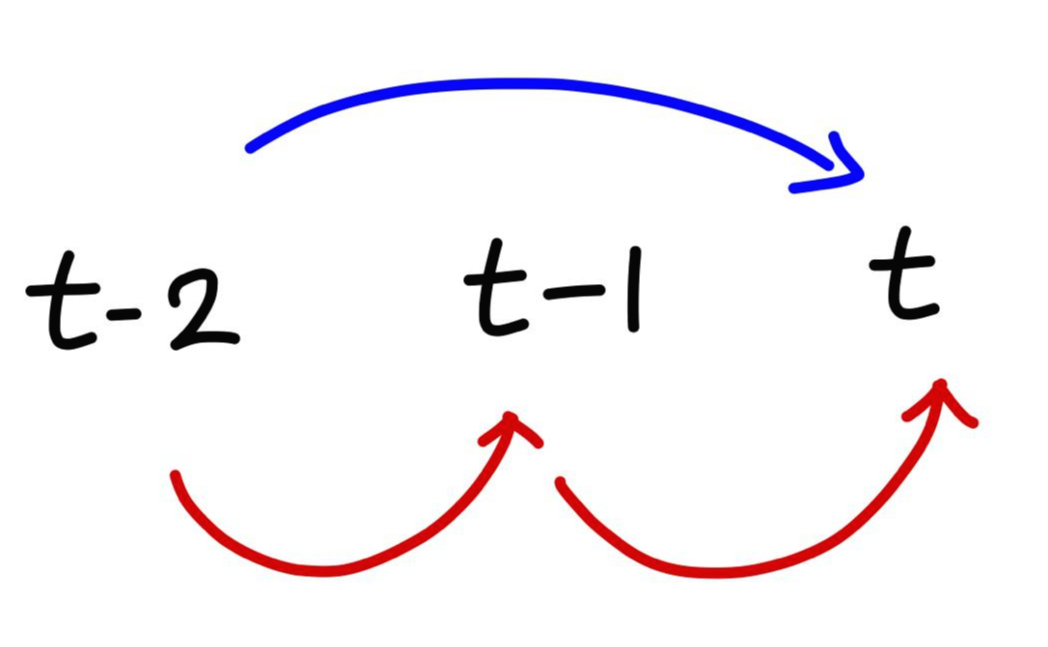
위와 같이 lag가 2인 경우에 대해 살펴보면, t기를 예측하기 위해 t-2기의 정보를 바로 사용할 수도 있고 (파란 선) , t-2기의 정보를 t-1기에 반영하고 t-2기의 정보가 반영된 t-1기의 정보를 반영함으로써 간접적으로 정보를 사용할 수도 있습니다 (빨간 선) 이 때 빨간선과 파란선 모두에 대한 상관계수를 구하는 것이 ACF이고, 파란 선에 대한 것만을 반영하는 것이 PACF입니다.
즉, 다른 변수를 모두 제외하고 오로지 y_t 와 y_(t-k) 의 관계만을 파악하는 것이 PACF입니다.
명확하게 와 닿지 않아 한가지 예를 들면, 마트에서 사과 판매액을 구하는 경우, 만약, lag =2 일 때 마다 이벤트를 한다면 t-1기를 거치면서 t-2기의 정보가 퇴색될 수 있으니, 아예 이런 점을 배제하고 생각하겠다는 것입니다... ㅎㅎ 일단 여기에선 데이터를 살펴보기 보단 어떤 방식으로 사용할 수 있는지만 알아보도록 하겠습니다.
from statsmodels.graphics.tsaplots import plot_pacf
Plot acf와 마찬가지로 먼저 이렇게 해당 library를 import해주셔야 사용할 수 있습니다.
plot_pacf(data, lags=20)
plt.show()그리고나서는 위의 코드를 사용해서 간단하게 pacf그래프를 그릴 수 있습니다.
AR Model
AR 모델은 Auto Regressive model (자기 회귀 모형) 의 약자로 자기 자신의 과거 데이터를 바탕으로 미래 데이터를 예측하는 모델을 의미합니다. 수식이 너무 많아 필기로 설명하겠습니다.

간단하게만 코드를 설명하자면, ARMA 모델을 쓰기 위해선 아래와 같이 라이브러리와 함수를 import 해주셔야합니다.
AR모델만을 사용하고 싶을때에는 ARMA모델을 사용한 뒤, MA모델의 차수를 0으로 설정하면 됩니다.
from statsmodels.tsa.arima_model import ARMA
model = ARMA(data, order=(1,0))
result = model.fit()아래와 같이 ARMA의 parameter로 모델을 돌리고 싶은 데이터를 집어넣어주고 order에 AR모델의 차수를 정해주면 됩니다. 이 때, order 뒤에 들어가는 튜플 중 앞의 값은 AR모델의 차수를, 뒤의 값은 MA모델의 차수를 의미합니다.
지금 제가 설정한 모델은 AR(1)모델이지만, plot_pacf를 통해서 어떤 차수를 넣을 지 확인 후 적절한 차수를 넣어주면 됩니다.
pacf를 그릴 때, 파란 박스 바깥에 있는 부분은 유의미한 의미를 가진다고 판단을 하고, 그 때의 lag를 차수로 넣으면 됩니다.

위 그림은 아래 summary에 들어가는 데이터에 대한 plot_pacf입니다. 이때 lag가 0일 때를 제외하고는 파란 부분 밖에 존재하는 것은 lag가 2일 때, 7일 때 밖에 없습니다. 그래서 저는 AR모델의 차수를 7로 하는 것이 좋겠다고 판단을 하여 AR(7)에 대해 모델을 돌렸습니다. 나머지는 아래 summary에서 확인해보겠습니다.
print(result.summary())
print(result.params)
위의 코드를 사용하면 내가 AR모델에 대해서 summary와 parameter를 확인할 수 있습니다.
밑에서 보여드리는 그림은 예시를 위해 제가 임의적으로 넣은 데이터로 위와 다르게 AR(7)차로 진행하였습니다.
코드에 관한 리뷰를 길게하면 블로그가 너무 길어질 것 같아서 일단 개념 설명을 위주로 하려고 가져온 데이터이니 참고로만 봐주세요!

일단 간략하게만 설명하자면, 1이라고 적힌 박스에서는 AR(7) 모델로 현재 데이터를 돌렸다는 것을 알 수 있습니다.
그리고 2를 보면 각 항 별 자기회귀계수를 알 수 있습니다. 맨 위에 적힌 const는 뮤 즉 평균을 의미하는데, 저는 위에선 식을 간편하게 만들기 위해 0라고 했는데 그 때 생략한 부분이라고 볼 수 있습니다.
그리고 t-1 에서의 계수 부터 t-2, t-3,, 차례로 t-7에서의 계수 (coef 라고 써진 주황색 박스) 를 알 수 있습니다. 이 때 그냥 넘어가지말고 p값을 봐야하는데 (p >abs(z)) 부분, 이 때 p값이 0.05 이하여야 유의미한 의미를 가진다고 할 수 있습니다. 이 때 위의 pacf 에서 유의미한 값을 가진다고 했던 lag=2,7 일때만 p값이 0.05 이하인 것을 확인할 수 있습니다. 즉, AR 차수를 2와 7로 해서 모델을 만들어야한다는 것을 알 수 있습니다.
마지막으로 AIC / BIC 는 각각 Akaike Information Criterion과 Bayesian Information Criterion 의 약자로 간단하게 말해서 해당 모델의 성능(?) 을 나타내고 저 값이 작을 수록 더 좋은 모델이라고 보통 봅니다.
(더 자세한 내용은 각자 찾아보시면 될 것 같습니다.)
위 그림은 summary() 함수에 대한 부분이고, params를 하게 된다면, 저 summary부분에서 coef 부분만을 따로 보여주는 함수입니다.
만약, 기회가 된다면 실제 ARMA모델로 test train set을 분리하여, 모델에 넣어 예측하고, 정확성을 측정하는 포스트(?) 를 새로 파겠습니다..ㅎㅎ
MA Model
MA 모델은 Moving average 라는 의미로 과거 오차들의 합으로 현재 데이터를 나타낼 수 있음을 의미합니다.

MA 모델도 위의 AR 모델과 유사하게 작용하는데 ARMA(data, order=(0,q) 이런식으로 order에서 AR모델의 차수를 지정하는 부분은 비워두시고, 내가 원하는 MA모델의 차수를 q 자리에 입력하면 됩니다. 나머지는 모두 AR모델과 같으니 생략하겠습니다.
AR(1) = MA(infinite)

컴퓨터로 수식을 적기가 어려워 손으로 적어봤습니다. AR(1)모델을 계속 연쇄적으로 나타내면 맨 밑의 모양과 같이 나옵니다. MA 모델은 과거의 에러 데이터를 바탕으로 현재의 데이터를 예측할 수 있게 하는 모델인데, AR(1)을 연쇄적으로 나타내게 되면 Y_t의 값은 에러들의 합으로 나타낼 수 있습니다. 또, AR, MA모델에서 파이의 절대값은 1보다 작아야하는데 절대값이 1보다 작은 값을 몇번이고 제곱해도 1보다 작은 수가 나타나게 되므로, 정의에 어긋나지 않습니다.
ARMA Model
ARMA모델도 정말 위와 똑같은 모양으로 ARMA(data, order=(p,q)) 이렇게 order 부분 앞 쪽에는 내가 원하는 AR모델의 차수인 p 를, 뒤 쪽에는 MA 모델의 차수인 q를 넣어주면 완성됩니다.
다시 한 번 말하지만 plot_acf를 통해서는 q 를 plot_pacf를 통해서는 p를 찾을 수 있습니다. (rules of thumb.,,)
뭔가 급하게 마무리한 느낌이긴 하지만, 읽어주셔서 감사합니다.
다음번엔 오늘 공부한 내용을 실제 데이터로 예측해보거나 ARIMA 모델에 대한 개념정리를 해보겠습니다..
사실 시계열분석의 코드 자체를 사용하는 것은 어렵지 않은데 (이미 너무 완벽한 라이브러리들이 많이 만들어져있어서..) 개념을 이해하기가 어려운 것 같아서 이번에는 실제 데이터를 가지고 직접 코드를 돌려보기 보단, 개념을 확실하게 알자! 라는 의미로 개념에 대한 정리 위주로 했습니다...
※ 제가 블로그를 시작한 이유는 타인에게 정보를 전달하기 위한 목적보다는 제가 공부하는 내용을 기록하려는 목적이 더 크기 때문에 혹시 보시다가 틀린 부분이 있으면 편하게 알려주셨으면 좋겠습니다 :)
※ 또한 실력이 아직 좋은 편은 아니기에 혹시 누군가가 제 블로그를 보신다면 같이 공부해가는 느낌으로 보셨으면 좋겠습니다.
※ Datacamp에서 제공되는 시계열분석 강의를 기반으로 공부하고 있습니다.
'시계열분석' 카테고리의 다른 글
| prophet (0) | 2021.11.14 |
|---|---|
| ARIMA&SARIMA (0) | 2021.11.07 |
| Fitting the ARMA model (0) | 2021.10.10 |
| 시계열분석 _ 자기상관과 ACF (0) | 2021.09.25 |
| 시계열분석 기초(1) (1) | 2021.09.24 |



