시계열 분석을 공부를 어제 시작했는데 저는 여기서부터 벌써 막혀버렸네요...어렵다는 것은 알았지만 제가 생각한 것 보다 더 어렵네요..! 역시 거두절미하고 시작하겠습니다.
Auto correlation
먼저, 자기 상관(auto correlation) 은 자기 자신과 일정한 시점 뒤의 자기 자신 사이의 상관관계입니다.
아래식은 자기 상관 계수에 관한 식인데요, 보통의 상관계수와 마찬가지로 계수는 -1과 1사이에서 결정되며, 계수가 1에 가까울수록 강한 양의 상관관계, 계수가 -1에 가까울수록 강한 음의 상관관계를 가집니다. 이 때 양의 값을 가지면, 추세를 따름, 음의 값
을 가지면 평균 되돌림이라고 하기도 합니다.

위 식을 보면 k 가 lag를 의미한다는 것을 알 수 있습니다. 원래 데이터와 원래 데이터를 한 시기 지연시킨 데이터의 상관계수를 알고 싶으면 k에 1을 대입하면 됩니다.
식은 복잡해보이지만, 계산은 컴퓨터가 해주기때문에 상관없습니다 ㅎㅎ,,
먼저, 간단한 예제를 보기위해 sin 함수 위의 50개의 숫자와 정규분포를 따르는 50개의 난수를 생성해 새로운 변수를 만들어보겠습니다.
noise = np.random.normal(loc=0, scale=1, size=50)
time = range(0,50)
sin = np.sin((np.array(time))* np.pi / 180)
data= sin + noise
위의 그래프의 모양을 살펴보면 아래와 같은 모습을 띄는 것을 볼 수 있습니다.
위에서 생성한 그래프는 array형태이기 때문에 plot으로 그리기 위해선 먼저, dataframe의 형태로 바꿔줘야합니다!

일반적으로 상관관계를 구하려면 두개의 데이터가 필요하지만, 자기 상관 계수를 구하기 위해서는 하나의 데이터만 있어도 됩니다. autocorr()이라는 함수를 이용해 손쉽게 구할 수 있습니다.
print(df["data"].autocorr())
이렇게 간단하게 상관계수를 구하고 싶은 열을 지정하고 함수를 사용하면 됩니다. 가로안에는 지연시킬 시킬 정도를 입력할 수 있습니다. default값은 1입니다! 만약 4를 입력한다면, 4기 이후의 데이터와 원본 데이터의 상관관계를 확인할 수 있습니다. 위 실행의 결과값은 -0.016726428296335066 이 나왔네요. 혹시 lag값 별로 알고 싶으면 for 문을 돌려서 확인할 수도 있지만, 간단하게 acf함수를 사용해서 확인해볼 수 있습니다.
ACF _ auto correlation function
from statsmodels.tsa.stattools import acf
from statsmodels.graphics.tsaplots import plot_acf
먼저 acf를 활용하기 위해서는 statsmodels에서 제공하는 함수를 다운받아야합니다
acf_array = acf(df)
print(acf_array)
이렇게 acf를 실행하면 1-20까지 총 20개의 (default값) lag에 대한 auto correlation 값을 반환해줍니다.
df 뒤에 lags = N 을 입력하시면 총 N개의 값을 반환받으실 수 있습니다.
[ 1. -0.01609952 -0.21781694 -0.12855397 0.19072289 0.02443979 0.10611266 -0.24589642 0.19467725 0.15203078 0.03903127 -0.201902 -0.02270887 0.09573581 0.22353238 -0.20984207 -0.01088939 -0.06166618 0.09981736 0.02837623 -0.07928601 -0.12292672 0.16805964 -0.06530867 -0.12583915 -0.06066281 0.04547008 -0.01173845 -0.05533553 -0.14627712 -0.02217624 0.06504061 0.09696063 -0.09928437 -0.11302866 0.11349645 0.03930495 -0.1600857 -0.07086976 0.06636556 0.05413325]
결과는 위와 같이 나왔습니다. 그러나, 숫자가 너무 많아 명확하지 않아 plot을 한 번 그려보겠습니다. 이때는 plot_acf를 사용합니다.
plot_acf(sin_df, lags=25, alpha =0.05)
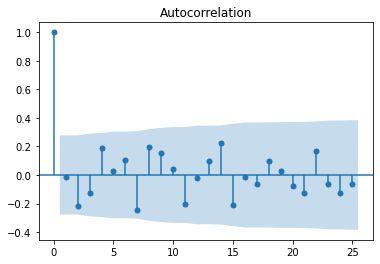
plt.show()이번에는 lags의 값을 25로 변경해봤습니다. 결과를 확인해보면 아래와 같은 결과가 나옵니다.

( lags=0 일때는 당연히 똑같은 데이터에 대한 상관계수를 구했기 때문에 1이겠죠..ㅎㅎ)
alpha는 신뢰구간을 설정합니다.. a = 0.05 는 95%의 신뢰구간을 가지는 것과 동일한 의미를 가집니다.
이 때 신뢰구간(파란 구간)을 벗어난다면 귀무가설을 기각할 수 있습니다.. (밑에서 더 설명하겠습니다.)
도대체 이 ACF가 어떻게 사용되며, 왜 필요한지에 대해 궁금해서 조금 찾아봤습니다.
ACF의 사용
먼저 시계열 데이터는 추세, 계절성, 주기를 포함하고 있습니다.
그런데 이 ACF를 사용하면 추세, 계절성, 주기의 존재를 파악할 수 있게됩니다. (나중에 ARIMA모델에서 중요한 계수로 사용된다는데, 아직 공부를 안해서 이건 ARIMA를 공부할때 다시 말씀드리겠습니다.)
만약, 추세가 존재한다면 ACF_plot은 감소하는 형태를, 계절성이 존재한다면 ACF-plot은 lag=4,8,12,16.. 등 4의 배수를 기준으로 가장 큰 값을 기록합니다 (분기별데이터 기준)
추세라는 것은 상승/ 하강하는 경향이기 때문에 lag가 짧으면 이전 데이터와 유사하게 움직이는 경향이 있기 때문에 lag가 작을수록 상관계수가 높고, lag가 커질수록 상관계수가 낮아지기 때문에 감소하는 형태가 나오고, 계절성이 존재한다면, 계절별로 비슷한 모양으로 움직이기 때문에 같은 계절끼리 비교하게 되는 4의 배수에서 (근방에서 가장)높은 값을 기록하는 결과가 나옵니다

위의 경우는 계절성이 두드러지는 데이터임을 확인할 수 있습니다.
이는 아래 다른 예시를 통해 다시 언급하겠습니다.
White noise
White noise는 자기상관관이 없는 시계열을 얘기합니다. 위에서 그렸던 ACF함수를 다시 가져와보면 무작위한 변동을 가지는 것을 알 수 있습니다. 이런 경우를 보통 White noise라고 하고, 이 White Noise 가 존재한다면, 과거를 통해 미래를 예측할 수 없습니다.
Random Walk
보통 주가는 랜덤워크를 따른다고 합니다.

위와 같이 어제의 가격에 random noise(shock)를 더한다면, 그것이 오늘의 가격이 되기 때문에 랜덤워크를 따른다고 볼 수 있습니다.
Adfuller
만약, 어떠한 식이 Randomwalk 인지 알고 싶어 가설을 새운다면, Adfuller을 이용해 이 가설을 검증해볼 수 있습니다.
from statsmodels.tsa.stattools import adfuller
adfuller 을 사용하기 위해선 함수를 import해줘야합니다. 그리고 내가 알고 싶은 데이터를 그 안에 넣으면 p값을 반환해줍니다.
(통계학적 지식에 대해서는 생략하겠습니다)
아까 sin 함수로 그린 그래프가 랜덤워크인지 알고 싶으면 이렇게 adfuller안에 해당 프레임을 넣으시면 됩니다. 그럼 반환된 result값과 result[1] 값을 살펴보겠습니다.
result = adfuller(df)
print(result)
print(result[1])
아래와 같은 결과가 반환됩니다.
(-6.770378001215817, 2.651185834199116e-09, 0, 49, {'1%': -3.5714715250448363, '5%': -2.922629480573571, '10%': -2.5993358475635153}, 110.28514559990039)
2.651185834199116e-09
이 때 result[1]은 p-value의 값을 반환해줍니다. 만약 p값이 0.05보다 낮았으면 귀무가설을 기각해서 랜덤워크가 아니라는 결론을 내릴수 있겠지만 p값이 2보다도 훨씬 크기때문에 해당 가설은 기각되지 않고 해당 데이터는 랜덤워크를 따름을 알 수 있습니다.
Resampling
아까부터 얘기하려고 했지만, 적절한 때를 잡지 못해서 이제야 얘기하네요 ㅎㅎ,, resampling은 인덱스가 Datetime으로 되어있는 경우에 사용하실 수 있습니다. 만약 내가 일별로 데이터를 모았다면 그 데이터를 주, 월, 년 별로 변환시켜주는 함수입니다. (시간에 대해서도 할 수 있지만 다루지 않겠습니다)
새로운 예시를 위해 제가 2011 - 2021 년의 S&P 500의 데이터를 다운받아왔습니다. (종가 데이터만 남김)

아래와 같은 모습으로 되어있습니다. 이 때, 일별 데이터가 아닌 월별데이터가 얻고 싶을때 resample을 사용할 수 있습니다.
SP500 = SP500.resample(rule = "M").last()
SP500
이 때 rule은 어떤 데이터로 resample할 것인가에 대한 parameter입니다. W는 한 주, M은 한 달, Q는 한 분기, A는 일년입니다. (annual) , 그리고 저 뒤에 last()는 가장 마지막 데이터만 남겨두겠다는 것을 의미합니다. mean, sum, first등을 사용할 수도 있습니다.
위의 데이터를 바탕으로 위에서 배운 것들을 써먹어볼까요?
SP500.plot()
plt.show()
먼저 어떤 개형인지 알아보기 위해 plot을 그려봤습니다.

오 매우 명확하게 추세를 따르는 것을 알 수 있습니다. 그럼 ACF를 통해 추세가 진짜 있는지 확인해볼까요?
plot_acf(SP500)
plt.show()
추세가 존재한다면, ACF그래프가 점점 감소하는 모습을 띤다고 했는데 정확하게 그런 모습을 그리는 것을 알 수 있습니다. 신기하네요 ㅎㅎ.. 그럼 해당 데이터가 랜덤워크를 따르는지 알아볼까요? Adfuller을 이용하겠습니다.
result1 = adfuller(SP500)
print(result1[1])결과는 0.9981815258263367 로 랜덤워크이다라는 귀무가설을 기각하지 못해 랜덤워크를 따르는 데이터임을 확인할 수 있습니다. SP500은 미국의 큰 기업(?) _언어구사능력이 약해서 ㅎㅎ 들 500개를 모아놓은 주가(?)를 나타내므로 랜덤워크를 따른다는 것이 상식과도 잘 맞음을 확인할 수 있습니다.
Stationary
드디어 마지막이네요 ㅎㅎ,, 블로그를 시작하니까 공부를 대충하지 않고 완전히 이해가 될 때까지 공부해서 좀 더 좋은 것 같네요.. 아무도 안보더라도 자기만족이 되네요 ㅎㅎ..
Stationary는 한국어로 정상성이라고 하는데 시계열 데이터가 시간에 관계없이 데이터가 관측되면 Stationary 라고 하고 그의 반대 데이터가 시간에 관계되어 있으면 Non - Stationary 데이터라고 합니다.
추세와 계절성이 있으면 데이터는 시간에 영향을 받기 때문에 Non - stationary 데이터라고 합니다.
시계열분석에서 다루는 ARIMA 모델을 다루기 위해선 non- stationary data 가 필요하기 때문에 이를 확인해야되는데요!아까 plot_acf를 그려봤다면, 계절성과 추세를 확인할 수 있는데요,,, 이때 diff() 함수를 이용해 간단히 제거할 수 있습니다. 위의 SP500은 추세를 포함한 non-stationary data 이기 때문에 diff()를 써서 detrending 해볼게요~
SP500 = SP500.diff()
SP500 = SP500.dropna()이렇게 diff()를 써서 간단하게 추세를 제거할 수 있습니다. diff()를 사용하게 되면 첫번째 행은 Nan 이 되기 때문에 dropna를 해서 행을 삭제해주셔야 됩니다. 그럼 plot_acf를 해볼까요?
plot_acf(SP500)
plt.show()결과는 아래와 같습니다. 아까와 다르게 추세가 제거된 것을 볼 수 있습니다.. 하하 원래 저게 저 파란범위 밖으로 나오면 안되는데,,, ㅎㅎ 더 공부해오겠습니다...

그리고 이 상황에서 돌려도되는지는 모르겠지만, 일단 adfuller를 돌려보면 p-value 는 1.5936838793409197e-15 으로 작은 수가 나와서 귀무가설을 기각할 수 있습니다. 즉 해당 데이터는 stationary 데이터라는 것을 알 수 있습니다! 그러면 이제 이 데이터를 모델에 돌릴 수 있습니다!
다음 블로그는 AR과 MA모델에 대해 공부해서 들고올게요 ㅎ,ㅎ,
혹시 누군가가 이 글을 다 봐주셨다면 정말 감사합니다 ㅎㅎ,,,
※ 제가 블로그를 시작한 이유는 타인에게 정보를 전달하기 위한 목적보다는 제가 공부하는 내용을 기록하려는 목적이 더 크기 때문에 혹시 보시다가 틀린 부분이 있으면 편하게 알려주셨으면 좋겠습니다 :)
※ 또한 실력이 아직 좋은 편은 아니기에 혹시 누군가가 제 블로그를 보신다면 같이 공부해가는 느낌으로 보셨으면 좋겠습니다.
※ Datacamp에서 제공되는 시계열분석 강의를 기반으로 공부하고 있습니다.
'시계열분석' 카테고리의 다른 글
| prophet (0) | 2021.11.14 |
|---|---|
| ARIMA&SARIMA (0) | 2021.11.07 |
| Fitting the ARMA model (0) | 2021.10.10 |
| 시계열분석 _ ARMA모델 개념정리 (0) | 2021.10.03 |
| 시계열분석 기초(1) (1) | 2021.09.24 |



